PROBABILIDAD II
PROBABILIDAD
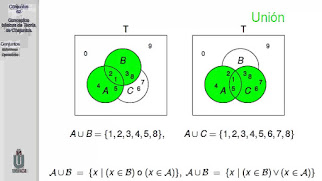
unión: En la teoría de conjuntos, la unión de dos conjuntos es una operación que resulta en otro conjunto, cuyos elementos son los mismos de los conjuntos iniciales.
Cuando la intersección de dos conjuntos es vacía, se dice que son disyuntos
y se representa S ∩ D = Ø.
El símbolo con el que se representa la intersección es este: ∩ se llama capa
por ejemplo:
F = {Amarillo, Azul, rojo, verde. morado}
G = {verde, café, rosado, negro, gris, rojo}
ENTONCES F ∩ G = { verde, rojo} ya que son los elementos que se repiten en ambos conjuntos.
A = { a, b, c, d, e} y B = { a, e, i, o}
Así, por ejemplo, si A = { a, b, c, d, e } y B = { a, e, i, o }, entonces la diferencia de dichos conjuntos estará formada por todos los elementos que estén solamente en A, esto es:
A – B = { b, c, d }
A la derecha, se representa dicha diferencia.
- Dos sucesos se dicen compatibles si tienen algún suceso elemental común. En este caso A∩B≠Ø, pueden ocurrir a la vez.
- Dos sucesos se dicen incompatibles si no tienen ningún suceso elemental común, en este caso A∩B=Ø y no pueden ocurrir a la vez
Un suceso y su contrario son siempre incompatibles, pero dos sucesos incompatibles no siempre son contrarios.
ejemplo:
- Suceso A = salir un número par = {2, 4, 6}
- Suceso B = salir un número impar = {1, 3, 5}
- Ambos sucesos no tienen sucesos elementales en común, por lo que son incompatibles.
Técnicas de conteo
- Paso 1: Definiendo el grupo de trabajo.
- Paso 2: Definiendo el elemento central.
- Paso 3: Las ramas de primer nivel.
- Paso 4: Primer verificación.
- Paso 5: Repetimos paso 3 y 4.
- Paso 6: Verificación final.
- elementos: Normalmente, la estructura de un diagrama de árbol consta de elementos como nodo raíz, un miembro que no tiene superior/padre. Luego están los nodos, que están conectados entre sí con conexiones de línea llamadas ramas que representan las relaciones y conexiones entre los miembros.
- diagrama de venn: Un diagrama de Venn usa círculos que se superponen u otras figuras para ilustrar las relaciones lógicas entre dos o más conjuntos de elementos. A menudo, se utilizan para organizar cosas de forma gráfica, destacando en qué se parecen y difieren los elementos.
- Un diagrama de Venn usa círculos que se superponen para ilustrar similitudes, diferencias y relaciones entre conceptos, ideas, categorías o grupos. Las similitudes entre los grupos se representan en las partes de los círculos que se superponen, mientras que sus diferencias se representan en las partes que no lo hacen.
De un grupo de 100 alumnos, 47 no han escogido informática como optativa, 56 no han escogido teatro como optativa y 27 no han escogido ni informática ni teatro. ¿Cuántos alumnos han escogido sólo un curso?
En primer lugar dibujamos el diagrama de Venn, con los dos conjuntos, informática y teatro, e indicando que el conjunto universal es igual a 100 alumnos:
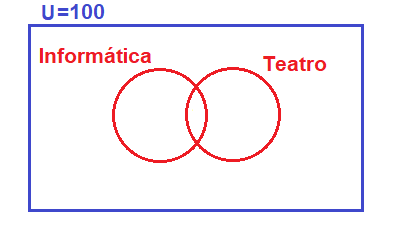
En estos tipos de ejercicios la clave está en ubicar los datos del enunciado dentro del diagrama de Venn.
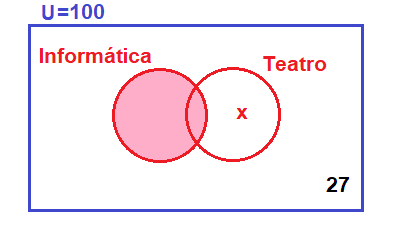
En este caso, el primer dato que vamos a ubicar son los 27 alumnos que no han escogido ninguno de los dos cursos, que corresponde a la zona 4 que hago referencia en la teoría de la lección:
He empezado por este dato porque sin él, no es posible ubicar el resto de datos del ejercicio.
Ahora vamos a ubicar los alumnos que no han escogido informática. Para ello, coloreo los alumnos que sí han escogido informática y lo que me queda, debe ser igual a 47 alumnos. Como ves, me quedan los 27 alumnos que no han escogido ningún curso y los alumnos que han escogido sólo teatro y como no conozco su valor, le llamo x:
Por tanto, los 47 alumnos que no han escogido informática, será igual a x alumnos que han escogido sólo teatro más los 27 que no escogieron nada:
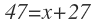
De esta ecuación despejamos x y me queda:
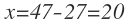
Por tanto, tenemos que 20 alumnos escogieron sólo teatro.
Seguimos ubicando los alumnos que no han escogido teatro. Para ello, coloreo los alumnos que sí han escogido teatro y lo que me queda, debe ser igual a 56 alumnos. Como puedes observar, me quedan los 27 alumnos que no han escogido ningún curso y los alumnos que han escogido sólo informática, que como no conozco su valor, le llamo «y»:
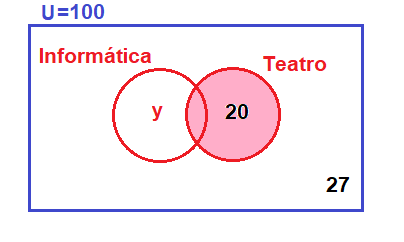
Los 56 alumnos que no han escogido teatro, será igual a «y» alumnos que han escogido sólo informática más los 27 que no escogieron nada:
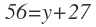
De esta ecuación despejo «y»
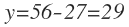
Por tanto, tenemos que 29 alumnos escogieron sólo informática, que lo añado en el diagrama de Venn:
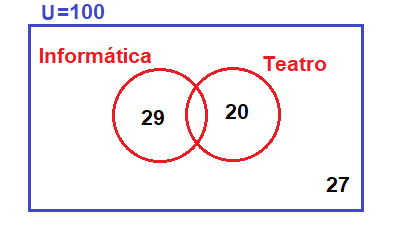
Me preguntan cuántos alumnos han escogido sólo un curso, que será la suma de los alumnos que escogieron sólo informática más los alumnos que escogieron sólo teatro:
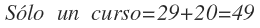
Por tanto, 49 alumnos han escogido sólo un curso.
- permutaciones y combinaciones: Las permutaciones son agrupaciones en las que importa el orden de los objetos. Las combinaciones son agrupaciones en las que el contenido importa pero el orden no. Dos eventos son dependientes si el estado original de la situación cambia de un evento al otro, y esto altera la probabilidad del segundo evento.
- Podemos dividir el número de permutaciones entre 6 y obtener el número de combinaciones. Esto es válido en general: Para encontrar el número de combinaciones de k objetos tomados de n objetos, dividir el número de permutaciones de escoger k de n objetos entre el número de permutaciones para escoger k de k objetos.
Una permutación de un conjunto de elementos, es una disposición de dichos elementos teniendo en cuenta el orden. El número de permutaciones de “n” elementos tomados de “k” en “k” se calcula con la fórmula:
Ejemplo 1:
Eduardo, Carlos y Sergio se han presentado a un concurso de pintura. El concurso otorga $200 al primer lugar y $100 al segundo. ¿De cuántas formas se pueden repartir los premios de primer y segundo lugar?
Solución:
En este caso, si importa el orden, ya que no es lo mismo quedar en primer lugar que en segundo, además, los premios son diferentes. Por ejemplo, un arreglo o disposición, es que Carlos ocupe el primer lugar y Sergio el segundo. Otro arreglo, sería que Sergio ocupe el primer lugar y Eduardo el segundo. El número total de arreglos o formas lo calculamos con la fórmula:
Combinaciones
Una combinación de un conjunto de elementos, es una selección de dichos elementos sin tener en cuenta el orden.
El número de combinaciones de “n” elementos tomados de “k” en “k” se calcula con la fórmula:
Ejemplo 2:
Un chef va a preparar una ensalada de verduras con tomate, zanahoria, papa y brócoli. ¿De cuántas formas se puede preparar la ensalada usando solo 2 ingredientes?
Solución:
En este caso, no importa el orden en que se tomen los ingredientes para la ensalada, pues da igual si es una ensalada de tomate con zanahoria, que una ensalada de zanahoria con tomate, ya que al final, el chef mezclará los dos ingredientes.
Un arreglo podría ser zanahoria y tomate, otro arreglo podría ser tomate y papa, otro arreglo podría ser papa y brócoli. El problema nos indica que solo se pueden usar 2 ingredientes en la ensalada. El número total de arreglos o formas lo calculamos con la fórmula:
- Lanzar una moneda y: Obtener cara. Obtener sello.
- Sacar una carta de un mazo y: Sacar un as. Sacar un 7. Sacar una reina. etc.
- Sacar una una canica de color de una bolsa y: Sacar una canica roja. Sacar una canica azul. Sacar una canica verde. etc.
- dependientes: Dos eventos son dependientes si el resultado del primer evento afecta el resultado del segundo evento, así que la probabilidad es cambiada. Ejemplo : La segunda oportunidad es un evento dependiente. Depende de lo que paso en la primera oportunidad.
- Los eventos independientes pueden incluir la repetición de una acción como lanzar un dado más de una vez, o usar dos elementos aleatorios diferentes, como lanzar una moneda y girar una ruleta. Para calcular correctamente las probabilidades, necesitamos saber si un evento influye en el resultado de otros eventos.
- independientes: En teoría de probabilidades, se dice que dos sucesos aleatorios son independientes entre sí cuando la probabilidad de cada uno de ellos no está influida porque el otro suceso ocurra o no, es decir, cuando ambos sucesos no están relacionados.
- Los eventos independientes pueden incluir la repetición de una acción como lanzar un dado más de una vez, o usar dos elementos aleatorios diferentes, como lanzar una moneda y girar una ruleta. Para calcular correctamente las probabilidades, necesitamos saber si un evento influye en el resultado de otros eventos.
- reforcemos lo aprendido:
Entonces, si gana será un resultado “éxito” y si pierde será un resultado “no éxito”. Esquemáticamente:
En la distribución binomial hay tres variables:
- n es el número de veces que repetimos el experimento.
- p es uno de los dos resultados al que llamaremos éxito.
- q es el otro resultado posible al que llamaremos fracaso
La probabilidad de cada posibilidad no puede ser más grande que 1 y no puede ser negativa. Por eso, como p y q son los dos únicos resultados posibles, entre los dos su porcentaje debe sumar uno, por lo que p =1- q.
La variable aleatoria que sigue una distribución binomial se suele representar como X~(n,p), donde n representa el número de ensayos o experimentos y p la probabilidad de éxito.
es el número de pruebas.
es el número de éxitos.
es la probabilidad de éxito.
es la probabilidad de fracaso.El número combinatorio
Fórmula
A la función distribución normal en la variable continua x, con parámetros μ y σ se le denota por:
N(x; μ,σ)
y explícitamente se escribe así:
N(x; μ,σ) = ∫-∞x f(s; μ,σ) ds
donde f(u; μ,σ) es la función densidad de probabilidad:
f(s; μ,σ) = (1/(σ√(2π)) Exp( – s2/(2σ2) )
La constante que multiplica a la función exponencial en la función densidad de probabilidad se le llama constante de normalización, y se ha elegido de tal manera que:
N(+∞, μ,σ) = 1
La expresión anterior asegura que la probabilidad de que la variable aleatoria x esté comprendida entre -∞ y +∞ sea 1, es decir el 100% de probabilidad.
El parámetro μ es la media aritmética de la variable aleatoria continua x y σ la desviación típica o raíz cuadrada de la varianza de esa misma variable. En el caso que μ = 0 y σ = 1 se tiene entonces la distribución normal estándar o distribución normal típica:
N( x; μ = 0, σ = 1)
probabilidad condicional
No tiene por qué haber una relación causal o temporal entre A y B. A puede preceder en el tiempo a B, sucederlo o pueden ocurrir simultáneamente. A puede causar B, viceversa o pueden no tener relación causal. Las relaciones causales o temporales son nociones que no pertenecen al ámbito de la probabilidad. Pueden desempeñar un papel o no, dependiendo de la interpretación que se le dé a los eventos.
Un ejemplo clásico es el lanzamiento de una moneda para luego lanzar un dado. ¿Cuál es la probabilidad que en el dado salga un 6 si ya ha salido una cara en la moneda? Esta probabilidad se denota de esta manera: .
El condicionamiento de probabilidades puede lograrse aplicando el teorema de Bayes.
La probabilidad condicional se calcula partiendo de dos sucesos o eventos (A y B) en un espacio probabilístico, indicando la probabilidad de que ocurra A dado que ha ocurrido B. Se escribe P (A/B), leyéndose como “probabilidad de A dado B”.
Si P(A) = 0,6 ; P(B) = 0,4 y P(A∩B)=0,18. Calcular:
a) P(A|B)
b) P(B|A)
Solución:
En este problema, simplemente vamos a reemplazar los datos en la fórmula.
a) Usamos la fórmula de probabilidad condicional:
b) Usamos la fórmula de fórmula de probabilidad condicional, teniendo en cuenta que vamos a calcular la probabilidad de que ocurra B, dado que ha ocurrido A.
Distribución de poisson
Distribución de Poisson: Es una distribución de probabilidad discreta, que expresa la probabilidad de un número k de eventos ocurriendo en un tiempo o espacio fijo si estos eventos ocurren con una tasa media conocida, y son independientes del tiempo o espacio desde el último evento.
Aquí algunos ejemplos típicos de variables aleatorias que siguen una distribución de Poisson:
- El número de clientes que ingresan a un supermercado en un día.
- El número de accidentes registrados en una fábrica durante una semana.
- El número de llamadas que recibe una central telefónica en el período de un minuto.
- El número de bacterias en un volumen de un litro de agua.
- El número de vehículos que llegan a una gasolinera en una hora.
- El número de fallas en la superficie de una pieza de cerámica rectangular.
- El número de toxinas en partes por millón encontradas en un litro de agua de un río.
teorema de Bayes
El teorema de Bayes es utilizado para calcular la probabilidad de un suceso, teniendo información de antemano sobre ese suceso. Podemos calcular la probabilidad de un suceso A, sabiendo además que ese A cumple cierta característica que condiciona su probabilidad.A esta se añade un suceso B cuya ocurrencia proporciona cierta información, porque las probabilidades de ocurrencia de B son distintas según el suceso Ai que haya ocurrido.
Conociendo que ha ocurrido el suceso B, la fórmula del teorema de Bayes nos indica como modifica esta información las probabilidades de los sucesos Ai.
Podemos calcular la probabilidad de un suceso A, sabiendo además que ese A cumple cierta característica que condiciona su probabilidad. El teorema de Bayes entiende la probabilidad de forma inversa al teorema de la probabilidad total. El teorema de la probabilidad total hace inferencia sobre un suceso B, a partir de los resultados de los sucesos A. Por su parte, Bayes calcula la probabilidad de A condicionado a B.El teorema de Bayes ha sido muy cuestionado. Lo cual se ha debido, principalmente, a su mala aplicación. Ya que, mientras se cumplan los supuestos de sucesos disjuntos y exhaustivos, el teorema es totalmente válido.
Fórmula del teorema de Bayes
Para calcular la probabilidad tal como la definió Bayes en este tipo de sucesos, necesitamos una fórmula. La fórmula se define matemáticamente como:
Donde B es el suceso sobre el que tenemos información previa y A(n) son los distintos sucesos condicionados. En la parte del numerador tenemos la probabilidad condicionada, y en la parte de abajo la probabilidad total. En cualquier caso, aunque la fórmula parezca un poco abstracta, es muy sencilla. Para demostrarlo, utilizaremos un ejemplo en el que en lugar de A(1), A(2) y A(3), utilizaremos directamente A, B y C.Una empresa tiene una fábrica en Estados Unidos que dispone de tres máquinas A, B y C, que producen envases para botellas de agua. Se sabe que la máquina A produce un 40% de la cantidad total, la máquina B un 30% , y la máquina C un 30%. También se sabe que cada máquina produce envases defectuosos. De tal manera que la máquina A produce un 2% de envases defectuosos sobre el total de su producción, la máquina B un 3%, y la máquina C un 5%. Dicho esto, se plantean dos cuestiones:
P(A) = 0,40 P(D/A) = 0,02
P(B) = 0,30 P(D/B) = 0,03
P(C) = 0,30 P(D/C) = 0,05
1.Si un envase ha sido fabricado por la fábrica de esta empresa en Estados Unidos ¿Cuál es la probabilidad de que sea defectuoso?
Se calcula la probabilidad total. Ya que, a partir los diferentes sucesos, calculamos la probabilidad de que sea defectuoso.
Expresado en porcentaje, diríamos que la probabilidad de que un envase fabricado por la fábrica de esta empresa en Estados Unidos sea defectuoso es del 3,2%.
2. Siguiendo con la pregunta anterior, si se adquiere un envase y este es defectuoso ¿Cuáles es la probabilidad de que haya sido fabricado por la máquina A?¿Y por la máquina B?¿Y por la máquina C?
Aquí se utiliza el teorema de Bayes. Tenemos información previa, es decir, sabemos que el envase es defectuoso. Claro que, sabiendo que es defectuoso, queremos saber cual es la probabilidad de que se haya producido por una de las máquinas.
P(A/D) = [P(A) x P(D/A)] / P(D) = [0,40 x 0,02] / 0,032 = 0,25
P(B/D) = [P(B) x P(D/B)] / P(D) = [0,30 x 0,03] / 0,032 = 0,28
P(C/D) = [P(C) x P(D/C)] / P(D) = [0,30 x 0,05] / 0,032 = 0,47
Sabiendo que un envase es defectuoso, la probabilidad de que haya sido producido por la máquina A es del 25%, de que haya sido producido por la máquina B es del 28% y de que haya sido producido por la máquina C es del 47%.
Vazquez Palacios Saraith
Comentarios
Publicar un comentario